6.8 Bernstein-Vazirani算法¶
6.8.1 Bernstein-Vazirani算法介绍¶
量子计算机是相对经典计算机而言的,量子计算机并不是在通常的计算问题上取代传统的电子计算机,而是针对特定问题完成经典计算机难以胜任的高难度计算工作。它是以量子力学为基础,实现量子计算的机器。比如:若运Deutsch-Jozsa 问题的量子算法(DJ算法),只需运行一次,就可以分辨函数是常数函数还是对称函数,而运用相应的经典算法则需要运行O(N)次才能达到该目的。 后来,Bernstein和Vazirani运用DJ算法有效地解决了询问量子数据库的 问题(即BV算法)。
问题描述:¶
经典算法情况:¶
由于对该函数的每个经典查询只能生成1位的信息, 而任意隐藏字符串 s 具有n位的信息, 所以经典查询复杂性是 \(O(n)\) 。
量子算法情况:¶
Bernstein-Vazirani的工作建立在Deutsch和Jozsa早期工作理论上来探索量子查询复杂度。他们对该领域的贡献是一个用于隐藏字符串问题的量子算法, 该算法的非递归量子查询复杂度仅为1,同比经典情况 \(O(n)\) 。这一量子算法的真正突破在于加快查询复杂度, 而不是执行时间本身。
案例:考虑n=3时的Bernstein-Vazirani问题。变量是3比特时,二进制表示为 \(x_0 x_1 x_2\) ,常数s则表示为 \(s_0 s_1 s_2\) ,因此所求的常数s总共有8个。此时,问题函数描述如下:
不难看出,对于经典算法而言,如果是 \(f_s (100)=s_0\) , \(f_s (010)=s_1\) , \(f_s (001)=s_2\) ,那么最少也需要3次调用函数才可以确定常量 \(s=s_0 s_1 s_2\) 。但是对于量子算法而言,使用下面的量子Oracle计算,1次就可以决定 \(s=s_0 s_1 s_2\) ,其计算复杂度为 \(O(1)\) 。
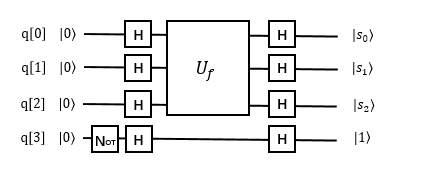
参考线路图:¶
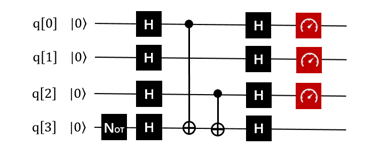
RX 3,"pi"
H 0
H 1
H 2
H 3
CNOT 0,3
CNOT 2,3
H 0
H 1
H 2
MEASURE 0,$0
MEASURE 1,$1
MEASURE 2,$2
这时,输出的结果,指代了s。通过验证,输出结果为:
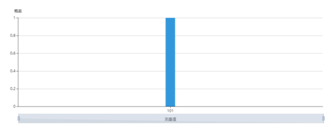
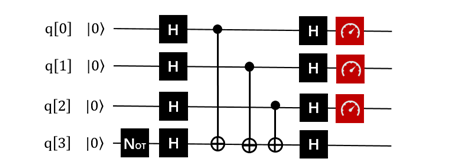
测量结果:
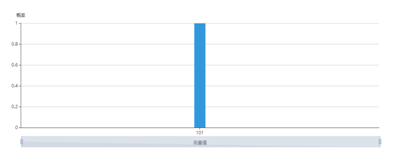
RX 3,"pi"
H 0
H 1
H 2
H 3
CNOT 0,3
CNOT 1,3
CNOT 2,3
H 0
H 1
H 2
MEASURE 0,$0
MEASURE 1,$1
MEASURE 2,$2
6.8.2 Bernstein-Vazirani算法的实现¶
下面给出 QRunes 实现 Bernstein-Vazirani 算法的代码示例:
6.8.3 Bernstein-Vazirani算法小结¶
Bernstein-Vazirani的工作建立在Deutsch和Jozsa早期工作理论上来探索量子查询复杂度。他们对该领域的 贡献是一个用于隐藏字符串问题的量子算法, 该算法的非递归量子查询复杂度仅为1,同比经典情况O(n)。这一量子算法的真正突破在于加快查询复杂度, 而不是执行时间本身。