6.2 Deutsch–Jozsa算法¶
6.2.1 Deutsch–Jozsa算法介绍¶
Deutsch–Jozsa算法是一种经过设计的情况,它证明了量子算法相对于经典算法有指数级别的加速能力。D-J算法的问题描述是这样的:
问题描述:
考虑函数:
\[f:\{0,1\}^n→\{0,1\}\]
我们保证有如下两种可能性:
- f是常数的(Constant), 即是对 \(x∈\{0,1\}^n\), 都有 f(x) = 0 或 f(x) = 1。
- f是平衡的(Balanced), 对于输入的 \(x∈\{0,1\}^n\), f(x)出输出0和1的个数相同。
算法的目标:判断函数f是什么类型。
经典算法情况:
在最简单的情况下,最少也需要2次才能判断函数属于什么类型。因为需要第二个输出才能判断最终函数的类型。对于n位输入时,最坏的情况下需要 \(2^{n-1}\) 次才能确认。
量子算法: 通过构造Oracle的方式,仅需运行一次就能确定函数属于哪一类。
植入步骤:
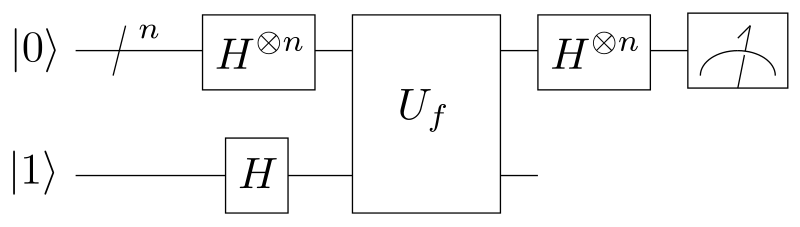
第一步,制备n个工作 (Working) 比特到 |0⟩ 态,与一个辅助 (Ancillary) 比特到 |1⟩。
第二步,所有比特都经过 Hadamard 变换,使系统处于叠加态上。
\[|0⟩^{⨂n} |1⟩^{H^{⨂n+1}}\rightarrow \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}|x⟩\left (\frac{(|0⟩-|1⟩)}{\sqrt2} \right)\]
第三步,系统通过Oracle ,一种酉变换,满足:
\[U_f:|x⟩|y⟩→|x⟩|y⊕f(x)⟩\]
这时候,系统状态为:
\[\frac{1}{\sqrt{2^n }}\sum_{x=0}^{2^n-1}|x⟩\left(\frac{(|0⟩ -|1⟩)}{\sqrt{2}}\right)\overset{oracle}{\rightarrow}\frac{1}{\sqrt{2^n }} \sum_{x=0}^{2^n-1}(-1)^{f(x)} |x⟩\left(\frac{(|0⟩ -|1⟩)}{\sqrt{2}}\right)\]
当f(x)=1时,会使得 \(\frac{(|0⟩-|1⟩)}{\sqrt{2}} →\frac{(|1⟩-|0⟩)}{\sqrt{2}}\),发生相位的翻转。
第四步:去除辅助比特,执行 Bell 测量。如果输出全部为0,则是f是常数的,反之,这是平衡的。
6.2.2 Deutsch–Jozsa算法的实现¶
下面给出 QRunes 实现 Deutsch–Jozsa 算法的代码示例:
6.2.3 Deutsch–Jozsa算法小结¶
经典算法的验证次数是 O(2^n) 的,量子算法算上叠加态的准备和测量的时间,需要的操作步骤为 O(n)。所以我们说明量子算法相对于经典算法具有指数级别加速的特性。 D-J算法的问题在于它解决的问题既不实用,又具有很大的限制(要求平衡函数中必须恰好为一半0一半1)。另外,我们还对黑盒子本身的形态有要求。所以说D-J算法的理论意义是远大于其实用意义的。